Exploring the squarified tree map algorithm with ReasonML (part 2)
Welcome to part two of this series of articles. In part one, we walked step-by-step through the inner workings of the squarified tree map algorithm using a concrete example. In this part, we’ll go over the actual implementation in ReasonML, or Reason for short. Along the way, we’ll discuss relevant concepts and features in the language. The purpose is to show how Reason can be used to elegantly solve a real world problem.
In case you are impatient, here is the full implementation. All functions in the code have corresponding unit tests. Here is an interactive notebook so you can play and experiment with the code. It contains a lot of the unit test cases as examples of how to use the functions.
Set up
Here are the setup steps:
yarn/npminstall the packagebs-platformglobally.- Initialize the project by running:
1bsb -init reason-squarify -theme basic-reason
- Add
jestas the unit testing framework as shown here.
After these steps, the repo should look like this.
Types
Coordinate system
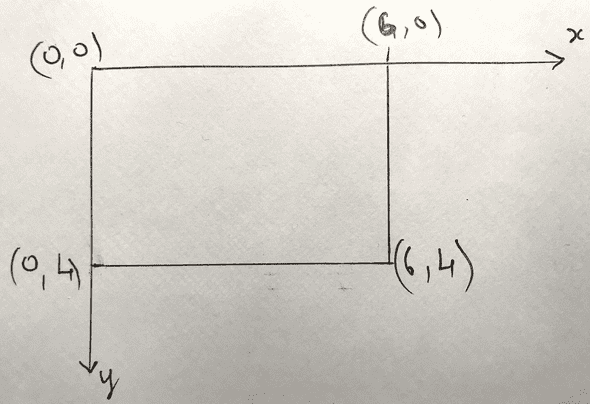
Recall from part one that our coordinate system follows the convention in a web browser: increases to the right and increases downward.
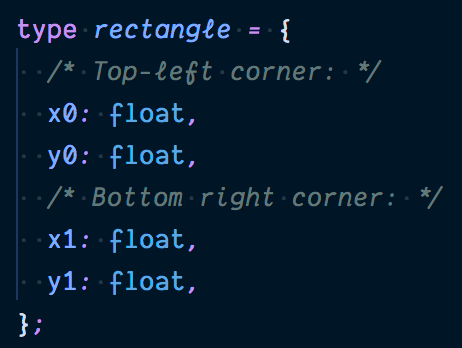
There are many ways to represent a rectangle in any algorithm and here we choose to specify the coordinates of the top-left corner ( and ) and bottom-right corner ( and ).
With that out of the way, let’s define a few types that will represent the various entities we’ll encounter. Types are an absolutely central part of any functional programming language and give these languages their expressive power. Based on the above convention, we define the type of a rectangle as follows:
Because Reason is just an alternative syntax for OCaml, Reason inherits OCaml’s two different types of numbers: float for floating-point numbers and int for integers.
However, because floating-point numbers are really the only effective type of number in our compilation target (JavaScript)1, we’ll represent all numbers in our Reason code as floats.
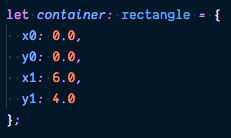
Given the above definition of a rectangle, this is how we represent the initial container in Reason:
This is called a let binding, which is how we declare variables in Reason.
Here we explicitly annotate the type of the container variable as rectangle.
Ordinarily, you can omit such a type annotation because the Reason compiler can infer the type of container by matching this binding against the closest compatible type definition i.e. rectangle.
In this article, we’ll choose to include more explicit type annotations than necessary to aid clarity.
Input data
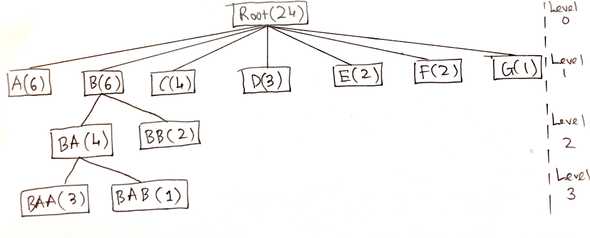
Recall from part one that our sample input tree looks like this
and the final output of the algorithm looks like this:
As noted at the end of part one, only leaf nodes (terminal nodes) remain in the visual output. Branch nodes (non-terminal nodes), which only indicate structural information e.g node contains nodes , and , have disappeared. As a result, I’ll chose a type representation for the input tree where leaf nodes contain the numerical value and label and branch nodes contain structural information. For example, leaf contains the numeric value and the label . On the other hand, branch contains the information that it is the parent of nodes and instead of directly containing the numerical value , which can be derived by summing up the values of ’s descendants.
With this mental model, we can define our tree data structure as follows:
In this snippet, the slightly right-slanted characters at the beginning of lines two and three are pipes (|), not forward slashes (/).
datum is a type that represents the data contained in each LeafNode:
There’s a lot to unpack in the definition of tree so let’s tackle it bit by bit.
The type tree is defined as a variant.
A variant type expresses the notion of disjunction: that a type can be “either this or that.”
We encounter variant types quite often in the physical world e.g. a lateral direction can be left or right, and Reason’s variant types allow us to model this behavior in an expressive way.
As will be seen later, Reason enforces the disjunctive nature of variants by requiring us to account for all the possible versions of a variant before using them in concrete computations.
By defining tree in this way, we’re saying a tree is recursive data structure that can either be a leaf node or a branch node.
Leaf nodes contain the label and numerical value information.
Branch nodes contain the structural information of the tree.
Each branch node contains a collection of more trees, represented as a list(tree).
We’ll discuss lists in the next section.
In the type definition of tree, LeafNode and BranchNode are called constructors.
Unlike class constructors in object-oriented languages, which perform necessary initialization tasks when new instances of a class are created, constructors in functional languages are a lot simpler.
You can think of them as mere wrappers around some data (or no data at all).
Here, LeafNode is a wrapper around a leaf node’s numeric value and label and BranchNode a wrapper around a collection of sub trees.
Based on this mental picture, our sample input tree can be represented as follows:
Unlike JavaScript, which allows string literals to be enclosed in either singe or double quotes, string literals in Reason must be enclosed in double quotes, a change that Douglas Crockford would surely approve.2
Output data
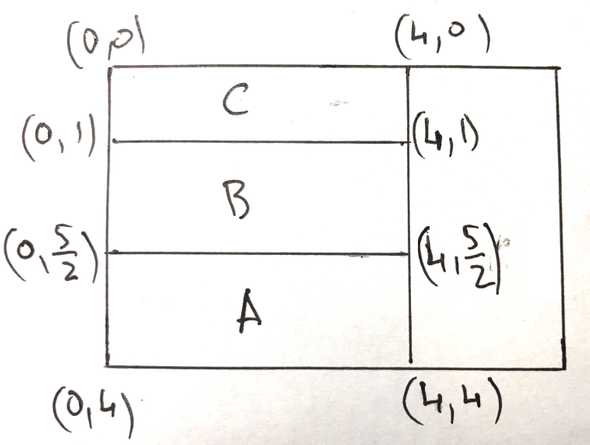
Recall from part one of this series that we call a collection of rectangles being laid out in the same orientation (horizontal vs vertical) a row. For example, the nodes , and form a row in the diagram below:
Our implementation will use lists to represent rows.
In Reason, a list is a homogenous and immutable collection of items.
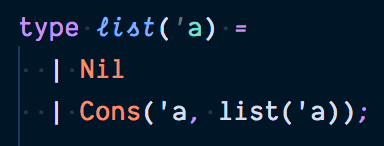
list can be thought of as a variant type:
which says that a list that holds value(s) of some type a (whatever it is) is either an empty list (Nil) or a “construct” (Cons) that holds a value of that type (called the head) plus another list (called the tail) containing values of the same type.
This definition makes Reason’s lists more like linked lists than JavaScript arrays.
Because lists are so widely used, Reason gives them some syntactic sugar: the empty list Nil is shortened to [] (empty square brackets) and the Cons pair is shortened to [head, ...tail].
In list’s definition above, a is called a type variable.
Similar to the way “value” variables express symbolic relationships between values e.g. and will be assigned concrete values at run time, type variables express symbolic relationships between types and will be assigned concrete values at compile time by the compiler, either through explicit type annotations by the developer or through type inference.3
For example, in this list of integers, the type variable a is int
Here we could have omitted the list(int) type annotation (usually read out loud as “list of ints”) because the compiler can infer it from the type of the literal values (1, 2, 3) in the list.
Based on our understanding of lists and the diagram above, we expect the output of our implementation to look like this:
where each cell adds the layout information (in the form of a rectangle) to the datum contained in the corresponding leaf node:
As noted above, branch nodes do not appear in the layout result.
Functions
The other central part of a functional language, other than types, is functions.
We’ll write a series of functions that progress from simple to complex, culminating in the two functions, squarify and traverse, that perform the breadth-wise and depth-wise recursions.
First off, how about a function that returns the shorter side of a rectangle?
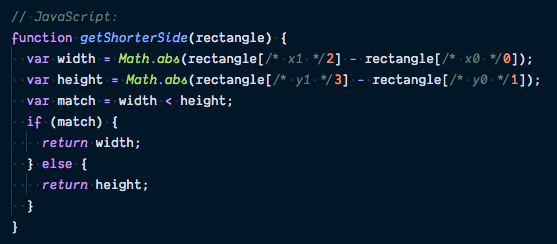
getShorterSide function

Functions in Reason look very similar to ES2015’s “arrow functions.”
They are defined with the parameters enclosed in parentheses on the left and the function body on the right of the “fat arrow” (=>).
There’s no return keyword because the value of the last statement is automatically returned.
In this case, the return value is the value of the last ternary statement, which works exactly the same as its JavaScript counterpart.
Because Reason makes a distinction between floats and integers, to perform arithmetic operations on floats, we have to use the dotted versions (+., -. etc) of the integer operators (+, - etc).
To calculate the width of the rectangle, we take the absolute value of the difference using the abs function.
Functions are invoked in Reason the same way in JavaScript: with arguments enclosed in parentheses.
Note that abs is neither in Reason’s built-in library nor implemented by us.
Rather, it’s a built-in function in JavaScript.
The first line in the screenshot (starting with [bs.scope) is an external4 (or inter-op) that says ”abs is function under the global Math scope that takes in a float and returns a float.”
In the JavaScript output, this external declaration will be erased and all references to abs in Reason will be replaced with Math.abs in JavaScript, as shown below:
This JavaScript output is very clean and readable and very close to what you would write by hand5. The easy inter-op with JavaSript and clean, readable output is one of Reason’s greatest strengths.
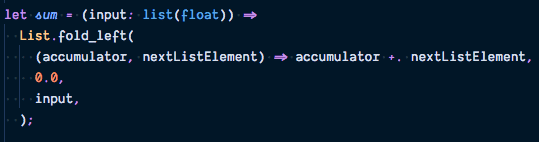
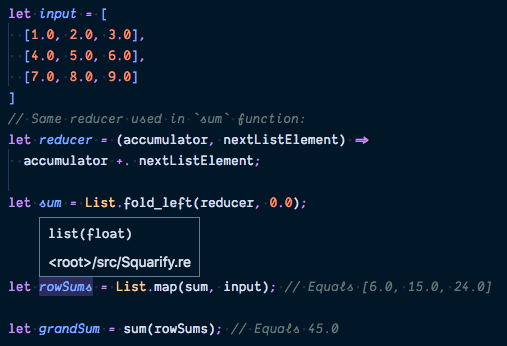
sum function
Another function that we’ll need later is sum that returns the sum of all elements in a list of floats:
List is a built-in module that contains utility functions to work with lists, one of which is fold_left.
We won’t cover modules in this article as it is a more advanced topic.
The function List.fold_left is very similar to the .reduce method on JavaScript’s arrays.
In fact, reduce is just another name for fold in functional languages.
List.fold_left takes three arguments 1) a function called the reducer that describes how to aggregate the list 2) the starting value of the aggregated value 3) the list itself.
And just like in JavaScript, functions, such as the reducer in this example, can be defined anonymously by listing the parameters followed by the function body, separated by the fat arrow =>.
sumValuesInTree function
Because only leaf nodes contain the numerical values, we need a way to sum up the values from all leaf nodes contained within a tree in order to do layout.
For example, if we run the input tree shown above through this function, we should get back 24.
Because the tree structure is recursive, performing operations on this tree naturally calls for a recursive function.
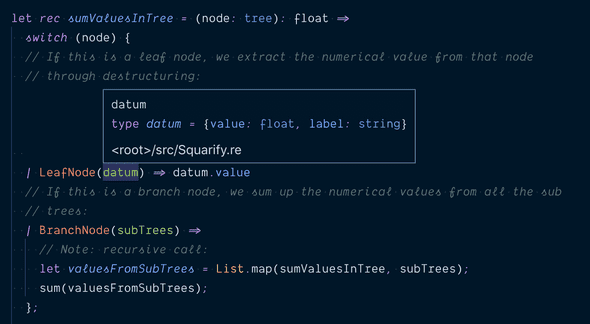
Because this recursive function calls itself, it has to be prefixed with the rec keyword as shown below:
This code introduces pattern matching via switch expressions.
Pattern matching allows us to check whether some piece of data has a certain structure and, if a match occurs, extracts parts of that data through destructuring, which is similar to destructuring an array or object in JavaScript.
We specify what data we want to match against by enclosing it in parentheses after the keyword switch and then list out all the cases, separated by pipes (|).
Each case consists of a pattern to the left of a fat arrow and what value to return from that pattern to the right.
One requirement of switch expressions is that the patterns must be exhaustive, that is, you must list all the possible patterns that the value being matched against can possibly have.
The combination of variants and exhaustive pattern matching is a very powerful feature of Reason and eliminates an entire class of programming bugs.
In this function, we use switch to match against the input node, which can be either a LeafNode or a BranchNode.
In the case of a LeafNode, we know that it contains a datum, which in turn contains the numerical value (as shown in the information tooltip).
In the case of a BranchNode, we know that it contains a list of subtrees so we use List.map to find the value sum of each sub tree.
List.map works in the same manner as the .map method on JavaScript arrays.
List.map takes in two arguments: a transformer and a list of items to be transformed.
List.map will use the transformer to transform every item in the input list and assemble all the output values into another list.
Thus, valuesFromSubTrees, the output of the List.map operation, is a list of floats because the input is a list of tree and the transformer transforms any tree into a float.
Applying the sum function to this list of floats gives us the sum of all the subtrees contained in the BrachNode.
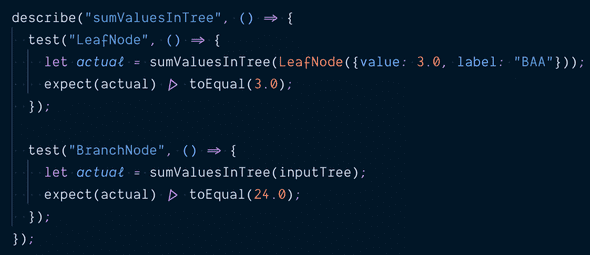
Below are two passing test cases from the test code.
When given the LeafNode with value , we expect the function to return .
When given the entire input tree, we expect to get back 6:
Partial application of functions
You might wonder about the peculiar ordering of the parameters of List.fold_left and List.map.
Why does the data comes last in the list of arguments and the iteratees come first?
To fully answer this question, let’s take a short detour.
Reason provides automatic partial application of functions.
That is, if a function is called with fewer arguments that it expects, the result is a function that can be called with some or all of the remaining arguments.
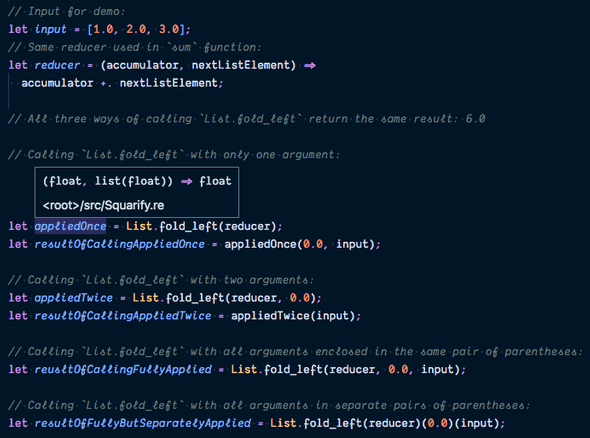
The screenshot below shows the many ways in which List.fold_left can be invoked to sum the list [1.0, 2.0, 3.0].
If we only provide the first argument, List.fold_left returns a function appliedOnce that takes in the remaining two arguments and returns a float (as shown in the information tooltip).
If we provide the first two arguments, List.fold_left returns a function appliedTwice that takes in the last argument and returns a float.
We get the final result only after supplying all three arguments.
We’re now in a position to answer the question posed at the beginning of this section.
In a language that provides automatic partial application such as Reason, the “iteratee-first data-last” ordering of arguments allows for more compact and expressive code.
In the snippet below, we use partial application to provide a more succinct definition of sum by conveniently leaving off the last argument of List.fold_left.
We can then use sum in multiple other places to sum up all numbers in the two-dimensional list input:
When applied to each row in input through List.map, that row becomes the last argument to List.fold_left, causing it to be fully applied and returns the sum for each row.
Note that Reason could infer that sum’s argument (equivalent to List.fold_left’s third argument) is a list of floats because the “plus” operation in the reducer function is the dotted i.e. floating-point version.
max function (two implementations)
A function max that takes in a list of floats and return the maximum value in that list sounds simple enough, but there is an edge case: what should the return value be if the input is an empty list?
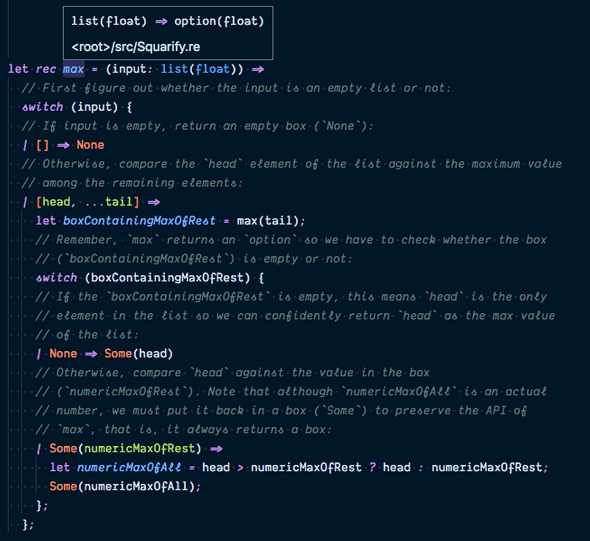
The idiomatic way in Reason, like in other functional languages, is to return a “box” that may or may not contain a maximum value and leave the consumer of the function to decide how to handle the case where the box is empty.
This notion of “a box that may or may not contain any value” is embodied by the built-in option type:
which says that an option of type a is a box that either contains nothing (None) or a value of type a (Some('a)).
With this edge case out of the way, here’s the function max.
This function uses pattern matching with switch twice.
In the first switch expression, we match against input, which is a list(float).
Recall from the previous section that a list can be either an empty list [] or an element followed by another list [head, ...tail].
In the second switch expression, we match against the return value of max, which is an option(float) that can be an empty box or a box that contains a float.
In case the box contains a float (numericMaxOfRest), the pattern allows us to extract the value numericMaxOfRest out of the box and uses it for comparison against head.
As it turns out, due to the way our program is structured, we do have the guarantee that the input list to max will have at least one element.
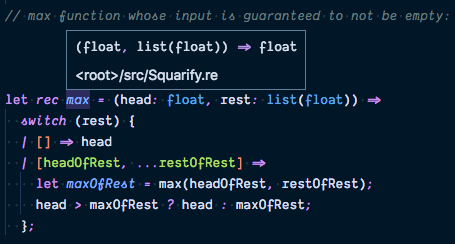
As such, we can simplify away the first switch expression (which checks whether the input is an empty list) so that max always return a float instead of option(float).
This is the version we’ll use in our final implementation:
The min function is defined in an almost identical way, which you can find in the code and won’t be reproduced here.
The more generalized max function we discussed earlier is still available as generalizedMax in the final code for your reference:
getMaxAspectRatioOfRow function
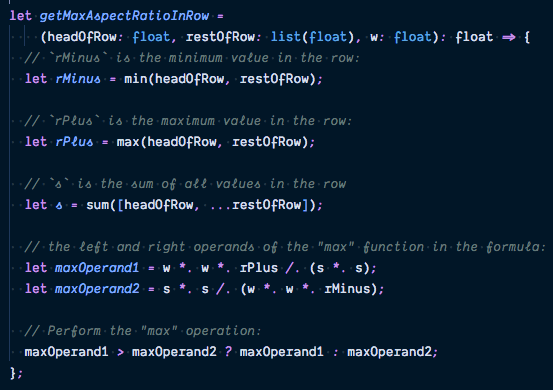
Whenever we consider whether to add a new tree node to the current row or to start a new one, we need to determine the maximum aspect ratio of the current row with and without the new added node. The formula to calculate the maximum aspect ratio of a row of nodes, as given in the paper, is
where:
- is the length of the side of the container along which we’re laying the rectangles out. As mentioned in part one, this is always the shorter side of the container.
- and are the maximum and minimum numerical values, respectively, of the nodes in the row.
- is the sum of the values of the nodes in the row.
- is a mathematical function that returns the larger of its two arguments.
It’s not the
maxfunction we implemented in Reason earlier, which returns the maximum value in a list.
Here is the implementation, which takes in the numerical values of the nodes in a row, represented as a list of floats, and the length of the container’s side (w).
Because we use the min and max functions defined earlier, which assumes the input list is not empty, the input row to getMaxAspectRatio must also be non empty.
As such, the input row is represented as a head node (headOfRow) followed by the rest of the nodes (restOfRow).
However, because the sum function takes in a list, we need to re-assemble headOfRow and restOfRow into a single list with the spread operator before passing them to sum.
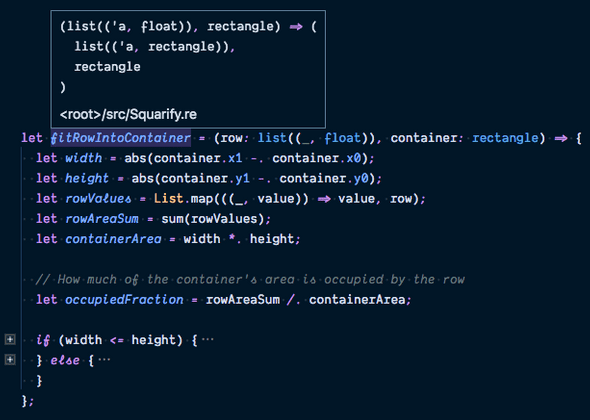
fitRowIntoContainer function
This function, fitRowIntoContainer, actually assigns each node its layout rectangle.
The function takes in a row to be laid out inside a container.
Each element in the row is a node accompanied by its numerical value.
The node-value association is done by putting the two in a tuple (in this case, a pair, or 2-tuple).
fitRowIntoContainer returns those same nodes, this time associated with their corresponding position in the layout.
The function also returns the portion of the container that remains unfilled after this layout step.
Here we encounter tuples for the first time.
They are immutable, ordered, fixed-size and heterogeneous collection of values.
For example, here is a tuple of a tree and a float:
and here is a list of such pairs, which are the row parameter to fitRowIntoContainer.
Note the double parentheses around ((tree, float)).
The inner one creates a tuple and the outer one encloses the type variable to the list:
Below is the first part of the function, where we figure out how much of the container is taken up by the nodes in the row:
You might have noticed that row is actually declared to have the type list((_, float)) instead of list((tree, float)).
The type _ in (_, float) conveys the idea that we don’t really care about the type of the first element of the tuple.
Indeed, this function simply “passes through” those first elements to the output without ever knowing what they are.
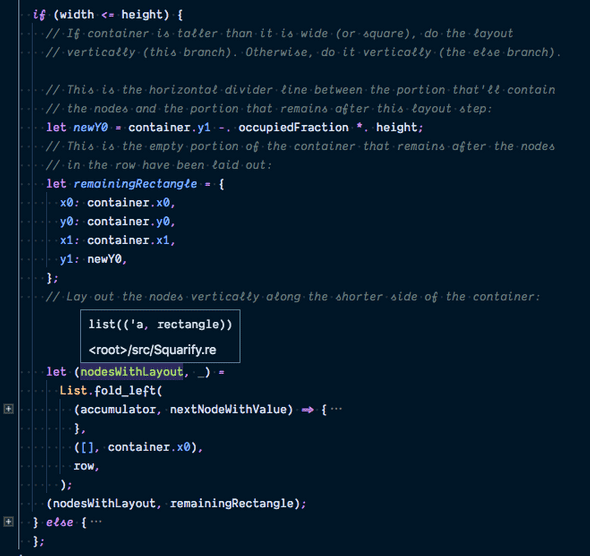
After figuring out the limit of the occupied area, we assign each node its own rectangular area one by one:
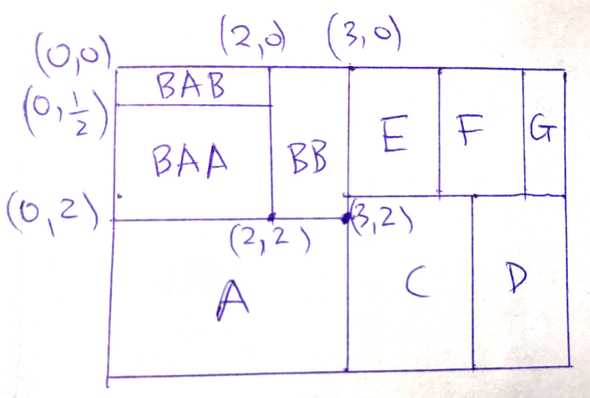
Although the code looks intimidating, we can get a sense for how it works by testing against the case of fitting nodes , and into the original container.
Here is the unit test that confirms the output coordinates match the visual diagram:
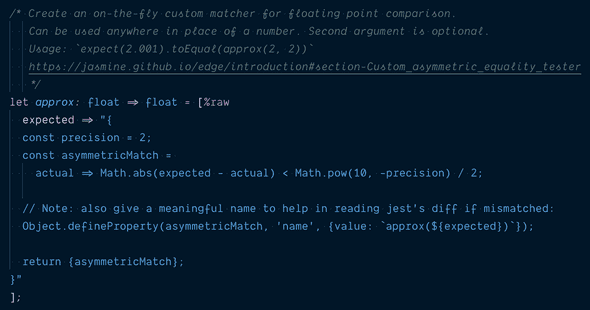
This is a quick aside about the approx function used in the unit test.
It’s a custom Jest/Jasmine asymmetric matcher that asserts that two float-point numbers are equal to within two decimal places:
Although approx is written in raw Javascript, Reason allows us to dump the JavaScript code directly in the middle of Reason code.
This capability means that when all else fails in the Reason world, you can always revert to writing JavaScript to “get things done,” an extremely important escape hatch in production code.
squarify function
Finally, we’re in the position to implement the squarify function that performs layout within a single level of the tree as demonstrated in part one of this series.
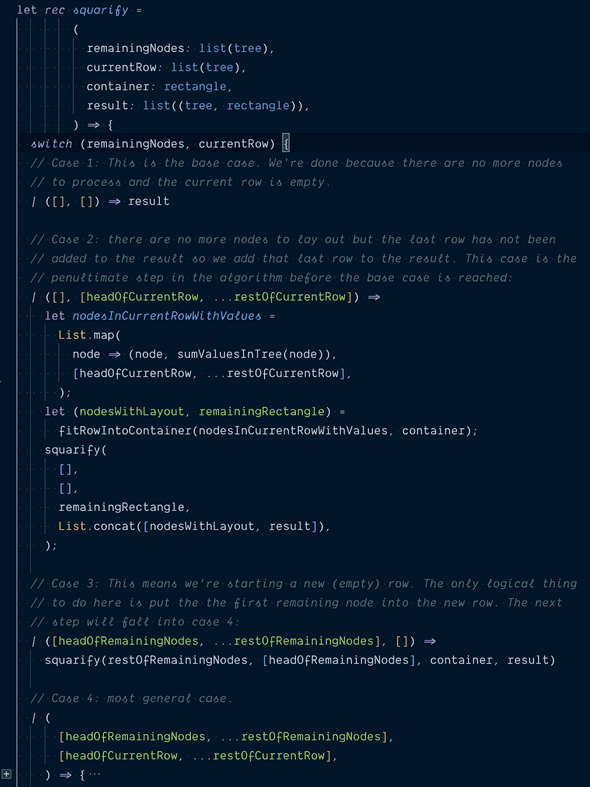
This is the function’s skeleton:
This function takes in four arguments:
remainingNodesis a list of nodes that haven’t been processed by the algorithm.currentRowis the list of nodes that have been accepted into the current row but not yet assigned a position in the layout.containeris a rectangle demarcating the current available space for layout.resultis the list of nodes that have already been assigned a layout position by the algorithm and will not be touched further.
The general flow of this recursive function goes like this.
One by one, it “shifts” the nodes from remainingNodes to the currentRow, stopping when the addition of the next node worsens the maximum aspect ratio of the currentRow.
At that point, all nodes in the currentRow will be assigned a rectangle within the container proportional to their values.
The nodes in currentRow will then be added to the result and the process starts anew with an empty currentRow and a new container.
This new container is the unfilled portion of the container from the last step.
Out of the four arguments to squarify, only the first three are true inputs because result plays the role of accumulating the results between recursive calls.
Out of these first three arguments, two are lists: remainingNodes and currentRow.
In order to process them, we are forced by Reason to account for whether or not they are empty lists, leading to four cases as annotated in the code.
These four cases turn out to be algorithmically quite meaningful.
- Case one, in which both
remainingNodesandcurrentRoware empty, is the base case of the recursion. Because there are neither nodes nor rows left to process, all nodes must already be in theresultlist, meaning we can return theresultlist as the final output of the algorithm. - Case two, in which
remainingNodesis empty butcurrentRowis not, corresponds to the penultimate step of the algorithm where the last row has been laid out but yet to be added to the result. The only thing left to do is to addcurrentRowtoresultand call the base case. - Case three, in which
remainingNodesis not empty butcurrentRowis, represents the moment when we are starting with a new row. The only logical action here is add the first node inremainingNodesto thecurrentRow. This will lead usually to case four but can also lead to case two. - Case four, in which both
remainingNodesandcurrentRoware not empty, is the most general case.
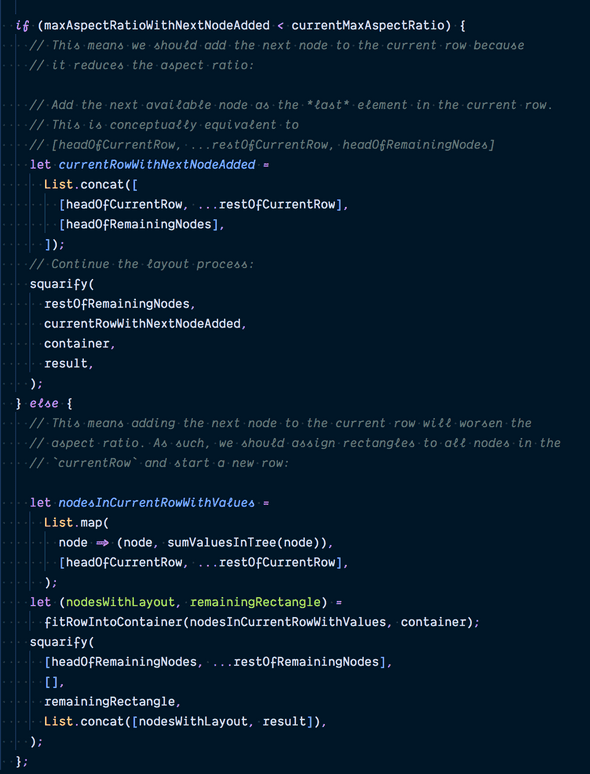
In the general case, we attempt to add the next remaining node to currentRow.
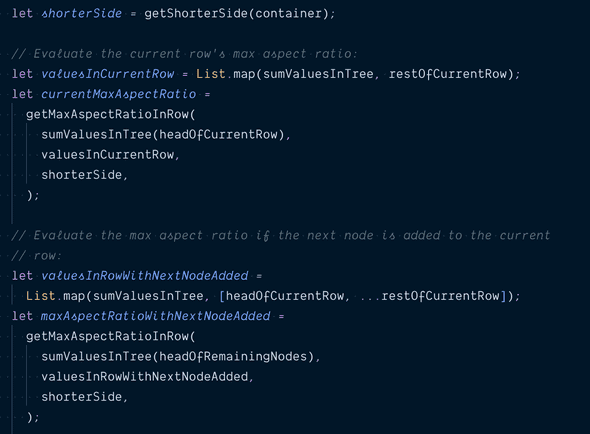
We first calculate the maximum aspect ratios of currentRow with and without the additional node by calling getMaxAspectRatioInRow:
By comparing these two numbers, we can decide whether to add it to the currentRow based on whether this addition improves the maximum aspect ratio:
Here is a small implementation detail that needs further explanation.
When we add a new node to a row, we add it to the end of that row.
If the current row is represented as [head, ...rest] and the next node to be added is is next, you can think of the new row with the added node as [head, ...rest, next].
However, this is not legal Reason syntax because the language only allows spreading at the end of a list.
The correct way is to use List.concat, which concatenates a list of lists together, like this:
Strictly speaking, we didn’t have to add a new node to end of the current row, which, due to the linked-list nature of Reason’s lists, is a linear-time operation. We could have just easily added to the beginning like this [next, head, ...rest], which is a constant time operation.
However, we decide to go with adding to the end to match the output in Bruls’ paper.
traverse function
This is the last function in the implementation.
As the name suggests, this function traverses the tree structure and perform the layout algorithm level-by-level.
It takes in an input tree and a container and returns a list of cells.
Its working is very similar to the sumValuesInTree function above.
If the function reaches a leaf node, there’s no more work to do.
If the function reaches a branch node, it performs the layout for all nodes at the top level in that branch node and descends into each branch to repeat the process.
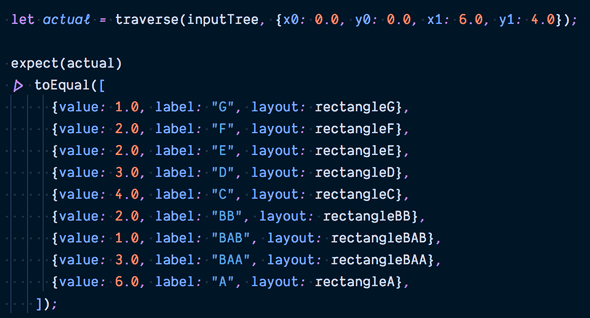
To cap it all off, here is the test case for traverse.
Let inputTree be the tree shown at the beginning of the article:
we expect the output of traverse to be a list consisting of only the leaf nodes in the tree accompanied by their final positions:
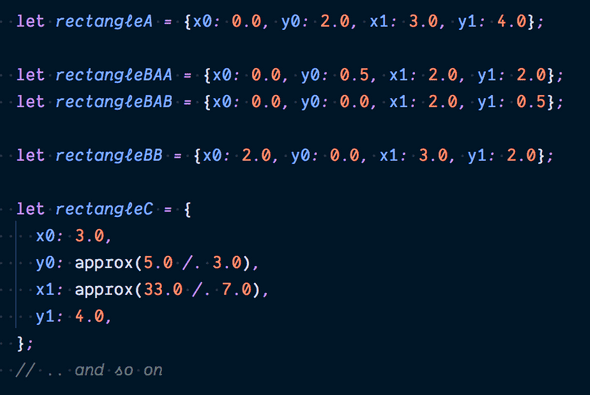
where the rectangles look like this:
Hopefully this article has given you a flavor of Reason when used to solve a real-world problem.
Because this implementation was written more as a pedagogical example than as a production code, there’s likely room for efficiency improvement, e.g. switching to tail-recursive List functions.
I’ve enjoyed using Reason a lot and I think it is a promising language to explore, especially in combination with React.
Out of all functional compile-to-JavaScript languages, Reason has the most familiar syntax to front-end developers, its JavaScript output is very readable and its type system (that of OCaml) has been battle tested over many years.
I’d like to thank J David Eisenberg for his very helpful feedback on this article.
- According to MDN, in JavaScript, all numbers are implemented in double-precision 64-bit binary format and integer values up to can be represented exactly. There’s no specific type for integers although
BigIntis an upcoming language proposal for representing integers that are very large.↩ - In this 2018 talk, he argues that JavaScript creates unnecessary clutter that leads to programming errors by allowing multiple ways to do things: tab & space for indentation, single & double quotes as delimiters for string literals,
null&undefinedas the bottom type and so on. He then proceeds to argue that we can remove this clutter by removing languages feature that we can do away with. For example, we should use double quotes for string literals because single quotes are already used as apostrophes.↩ - Reason uses a Hindley-Milner type system, which this article does a good job of explaining.↩
- Strictly speaking,
[bs.scope]is a construct specific to BuckleScript rather than Reason. Reason is the alternative Syntax for OCaml. BuckleScript is the compiler that compiles OCaml to JavaScript.↩ - An attentive reader might notice that in the JavaScript output, a
rectangleis represented as a JavaScript array instead of a JavaScript object (official rationale here and more discussion here) and that arectangle’s fields (x0,y0etc) are accessed by indexing into that array. What goes on under the hood is that the compiler keeps an internal record of what field name corresponds to what JavaScript array index and outputs the appropriate JavaScript indexing operations.↩ - The triangular-looking characters in the test code are the pipe operator
|>, which takes the item on the left and put it as the last argument of the item on the right. Suppose we have a functionf(a, b)that takes two arguments, the following two expressions are equivalent:b |> f(a)andf(a, b). This|>operator is also colloquially called “pipe last” to distinguish it from the “pipe first” operator->, which puts its left operand as the first argument of the function on its right:a -> f(b)is equivalent tof(a, b). Pipe operators are used in these tests to maintain the same visual semantics as Jest assertions written in JavaScript:expect(actual).toEqual(expected).↩